Binary numbers to BCD (bin_to_bcd), Hexadecimal Number to BCD (hex_to_bcd) Code Conversion and Application – zynq xc7z030 board – FII-PE7030 Experiment 7

January 7, 2020June 28, 2020 SteveGuysBCD Code, bitstream file, FII-PE7030, Hexadecimal Number, zynq xc7z030 board

Experiment 7 Hexadecimal Number to BCD Code Conversion and Application

Experiment Objective

Learn to convert binary numbers to BCD (bin_to_bcd)
Learn to convert hexadecimal numbers to BCD (hex_to_bcd)

7.2 Experiment Implement

Combined with experiment 6, display the calculation results on the segment display.

7.3 Experiment

7.2.1 Introduction to Hexadecimal Number to BCD Code Conversion

Since the hexadecimal display is not intuitive, decimal display is more widely used in real life.

Human eye recognition is relatively slow, so the display from hexadecimal to decimal does not need to be too fast. Generally, there are two methods

Countdown method:

Under the control of the synchronous clock, the hexadecimal number is decremented by 1 until it is reduced to 0. At the same time, the appropriate BCD code decimal counter is designed to increment. When the hexadecimal number is reduced to 0, the BCD counter just gets with the same value to display.

Bitwise operations (specifically, shift bits and plus 3 here). The implementation is as follows:
Set the maximum decimal value of the expression. Suppose you want to convert the 16-digit binary value (4-digit hexadecimal) to decimal. The maximum value can be expressed as 65535. First define five four-digit binary units: ten thousand, thousand, hundred, ten, and one to accommodate calculation results
Shift the hexadecimal number by one to the left, and put the removed part into the defined variable, and judge whether the units of ten thousand, thousand, hundred, ten, and one are greater than or equal to 5, and if so, add the corresponding bit to 3 until the 16-bit shift is completed, and the corresponding result is obtained.

Note: Do not add 3 when moving to the last digit, put the operation result directly

The Principle of hexadecimal number to BCD number conversion

Suppose ABCD is a 4-digit binary number (possibly ones, 10 or 100 bits, etc.), adjusts it to BCD code. Since the entire calculation is implemented in successive shifts, ABCDE is obtained after shifting one bit (E is from low displacement and its value is either 0 or 1). At this time, it should be judged whether the value is greater than or equal to 10. If so, the value is increased by 6 to adjust it to within 10, and the carry is shifted to the upper 4-bit BCD code. Here, the pre-movement adjustment is used to first determine whether ABCD is greater than or equal to 5 (half of 10), and if it is greater than 5, add 3 (half of 6) and then shift.

For example, ABCD = 0110 (decimal 6)

After shifting it becomes 1100 (12), greater than 1001 (decimal 9)
By plus 0110 (decimal 6), ABCD = 0010, carry position is 1, the result is expressed as decimal
Use pre-shift processing, ABCD = 0110 (6), greater than 5, plus 3
ABCD=1001(9), shift left by one
ABCD=0010, the shifted shift is the lowest bit of the high four-bit BCD.
Since the shifted bit is 1, ABCD = 0010(2), the result is also 12 in decimal
The two results are the same
Firstly, make a judgement, and then add 3 and shift. If there are multiple BCD codes at the same time, then multiple BCD numbers all must first determine whether need to add 2 and then shift.
The first way is relatively easy. Here, the second method is mainly introduced.

Example 1: bin_to_bcd

Figure 7.1 Example 1, bin_to_bcd

Example 2: Hex to BCD, the process is shown in Figure 7.2.

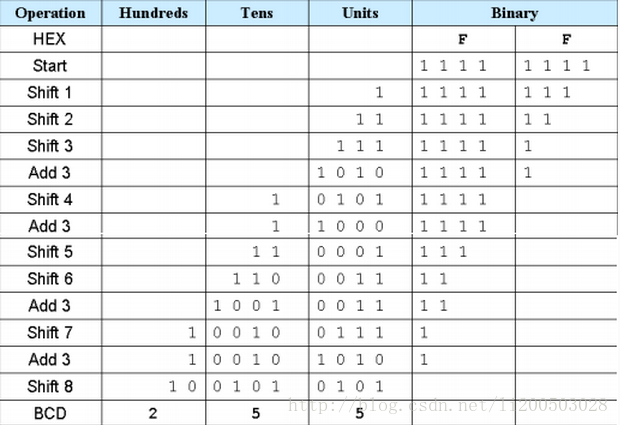
Figure 7.2 hex_to_bcd

7.2.2 Program Introduction

The first step: the establishment of the main program framework (interface design)

module HEX_BCD (

input [15:0] hex,

output reg [3:0] ones,

output reg [3:0] tens,

output reg [3:0] hundreds,

output reg [3:0] thousands,

output reg [3:0] ten_thousands

);

Enter a 16-bit binary number hex, which can represent up to 65535 in decimal, so output one-digit ones, ten-digit tens, hundred-digit hundreds, thousands digit thousands, and ten-thousand digit ten_thousands.

The second step: implementation of fast algorithm

reg [15:0] hex_reg;

integer i;

always @ (*)

begin

hex_reg = hex;

ones = 0;

tens = 0;

hundreds = 0;

thousands = 0;

ten_thousands = 0;

for (i = 15; i >= 0; i = i-1) begin

if(ten_thousands >= 5)

ten_thousands = ten_thousands + 3;

if(thousands >= 5)

thousands = thousands + 3;

if(hundreds >= 5)

hundreds = hundreds + 3;

if(tens >= 5)

tens = tens + 3;

if(ones >= 5)

ones = ones + 3;

ten_thousands = ten_thousands << 1;

ten_thousands[0] = thousands[3];

thousands = thousands << 1;

thousands[0] = hundreds[3];

hundreds = hundreds << 1;

hundreds[0] = tens[3];

tens = tens << 1;

tens[0]= ones[3];

ones = ones << 1;

ones[0] = hex_reg[15];

hex_reg = {hex_reg[14:0], 1’b0};

end

Referring to Figure 7.2, the first part of the program is the judgment and calculation part, if it is larger or equal to 5, add 3, and the latter part is the shift part.

The third step: verification

Refer to experiment 6, and use Modelsim for simulation. The simulation conditions are set as follows:

initial begin

hex = 0 ;

repeat (20) begin

#10;

hex = {$random}%20000;

#10;

end

At the beginning, the 16-bit binary number is equal to 0, and then it is delayed by 10ns. The 16-bit binary number is taken as a random number less than 20,000. The delay is ended after 10ns, and the entire process is repeated 20 times.

Refer to experiment 6. After running the simulation, the simulation results are shown in Figure 7.3.

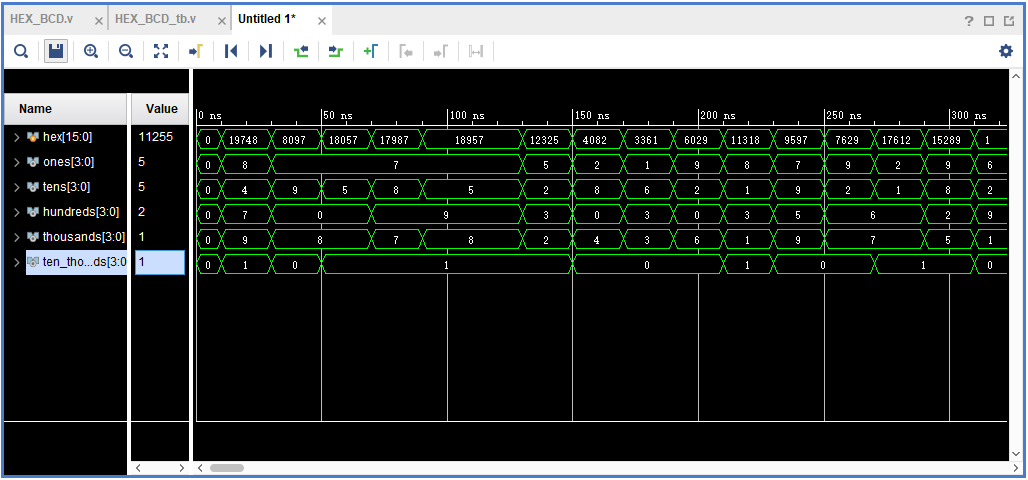
Figure 7.3 Simulation result

Application of Hexadecimal Number to BCD Code Conversion

Continue to complete the multiplier of experiment 6 and display the result in a segment display in decimal. Every 1s clock passes, the calculation result on the segment display changes once. The experiment requires frequency division, segment display, multiplier, and Hex to BCD conversion code. Refer to the previous experiments, and instantiate the parts in the new top level entity.

After completing the implementation, find and expand the IMPLEMENTATION option under the Flow Navigator window on the main interface of Vivado, expand Run Implementated Design, and click Report Timing Summary to view the circuit timing report. As shown in Figure 7.4, the timing requirements are satisfied.

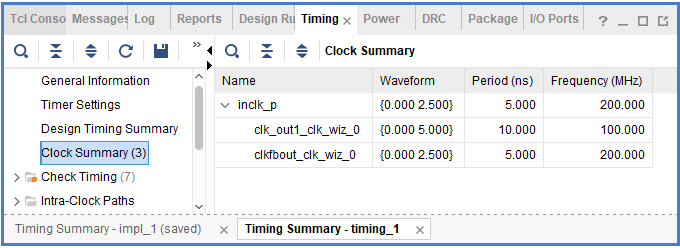
Figure 7.4 Timing report

7.5 Experiment Verification

The first step: add cosntraints and assign pins

The pin assignmnets are shown in Table 7.1.

Table 7.1 Hex to BCD conversion pin mapping table

Signal Name	Network Name	FPGA Pin	Port Description
inclk_p	SYSCLK_P	AC13	Input clock(differential) 200MHz
inclk_n	SYSCLK_N	AD13	Input clock(differential) 200MHz
sw[0]	GPIO_DIP_SW0	A17	8-bit switch
sw[1]	GPIO_DIP_SW1	E8
sw[2]	GPIO_DIP_SW2	C6
sw[3]	GPIO_DIP_SW3	B9
sw[4]	GPIO_DIP_SW4	B6
sw[5]	GPIO_DIP_SW5	H6
sw[6]	GPIO_DIP_SW6	H7
sw[7]	GPIO_DIP_SW7	G9
tube_sel[0]	SEG_D0	C1	Bit selection signal
tube_sel[1]	SEG_D1	E3
tube_sel[2]	SEG_D2	F7
tube_sel[3]	SEG_D3	D6
tube_sel[4]	SEG_D4	H11
tube_sel[5]	SEG_D5	J11
tube_seg[0]	SEF_PA	J10	Segment selection signal
tube_seg[1]	SEF_PB	J9
tube_seg[2]	SEF_PC	A7
tube_seg[3]	SEF_PD	B7
tube_seg[4]	SEF_PE	A8
tube_seg [5]	SEF_PF	A9
tube _seg[6]	SEF_PG	A10
tube _seg[7]	SEF_DP	B10

The second step: run the implementation, generate bitstream files, and verify the board

After successfully downloading the generated programmable bitstream file to the Zynq_7030 development board, the experimental phenomenon is shown in Figure 7.5.

The input value of the DIP switch is 00001010, and it is 10 in decimal. The counter keeps accumulating, so the display result also keeps increasing by 10.