Experiment 7 Hexadecimal Number to BCD Code Conversion and Application

Experiment Objective

1. Learn to convert binary numbers to BCD code (bin_to_bcd)
2. Learn to convert hexadecimal numbers to BCD code (hex_to_bcd)

7.2 Experiment Implement

Combined with experiment 6, display the results of the operation to the segment display.

7.3 Experiment

7.2.1 Introduction to the Principle of Converting Hexadecimal Number to BCD Code

Since the hexadecimal display is not intuitive, decimal display is more widely used in real life.

Human eyes recognition is relatively slow, so the display from hexadecimal to decimal does not need to be too fast. Generally, there are two methods

1. Countdown method:

Under the control of the synchronous clock, the hexadecimal number is decremented by 1 until it is reduced to 0. At the same time, the appropriate BCD code decimal counter is designed to increment. When the hexadecimal number is reduced to 0, the BCD counter Just gets with the same value to display.

1. Bitwise operations (specifically, shift bits and plus 3 here). The implementation is as follows:
2. Set the maximum decimal value of the expression. Suppose a 16-digit binary value (4-digit hexadecimal) needs to be converted to decimal. The maximum value can be expressed as 65535. Firstly five four-digit binary units are defined: ten thousand, thousand, hundred, ten, and one to accommodate calculation results
3. Shift the hexadecimal number by one to the left, and put the removed part into the defined variable, and judge whether the units of ten thousand, thousand, hundred, ten, and one are greater than or equal to 5, and if so, add the corresponding bit to 3 until the 16-bit shift is completed, and the corresponding result is obtained.

Note: Do not add 3 when moving to the last digit, put the operation result directly

1. The principle of hexadecimal number to BCD number conversion

Suppose ABCD is a 4-digit binary number (possibly ones, 10 or 100 bits, etc.), adjusts it to BCD code. Since the entire calculation is implemented in successive shifts, ABCDE is obtained after shifting one bit (E is from low displacement and its value is either 0 or 1). At this time, it should be judged whether the value is greater than or equal to 10. If so, the value is increased by 6 to adjust it to within 10, and the carry is shifted to the upper 4-bit BCD code. Here, the pre-movement adjustment is used to first determine whether ABCD is greater than or equal to 5 (half of 10), and if it is greater than 5, add 3 (half of 6) and then shift

For example, ABCD = 0110 (decimal 6)

1. After shifting it becomes 1100 (12), greater than 1001 (decimal 9)
2. By plus 0110 (decimal 6), ABCD = 0010, carry position is 1, the result is expressed as decimal 12
3. Use pre-shift adjustment, ABCD = 0110 (6), greater than 5, plus 3
4. ABCD = 1001 (9), shift left by one
5. ABCD = 0010, the shifted bit is the lowest bit of the high four-bit BCD.
6. Since the shifted bit is 1, ABCD = 0010(2), the result is also 12 in decimal.
7. The two results are the same
8. Firstly, make a judgement, and then add 3 and shift. If there are multiple BCD codes at the same time, then multiple BCD numbers all must first determine whether need to add 2 and then shift.
9. The first way is relatively easy. Here, the second method is mainly introduced.

Example 1: Binary to BCD. See Figure 7.1.

Figure 7.1 Example 1, bin_to_bcd

Example 2: Hexadecimal to BCD. See Figure 7.2.

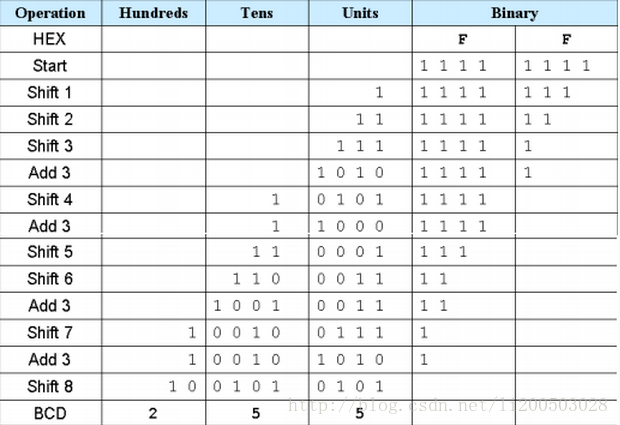
Figure 7.2 hex_to_bcd

7.2.2 Introduction of the Program

The first step: the establishment of the main program framework

module HEX_BCD (
	
	input		[15:0] hex,
	output	reg	[3:0]  ones,
	output	reg	[3:0]  tens,
	output	reg	[3:0]  hundreds,
	output	reg	[3:0]  thousands,
	output	reg	[3:0]  ten_thousands 
);

Enter a 16-bit binary number hex, which can represent a maximum of 65535 decimal, so output ones, tens, hundreds, thousands, and ten_thousands.

The second step: the implementation of bit operation

reg		[15:0]	hex_reg;	
integer			i;
always @ (*)
begin
	hex_reg = hex;
	ones = 0;
	tens = 0;
	hundreds = 0;
	thousands = 0;
	ten_thousands = 0;
	
	for (i = 15; i >= 0; i = i-1) begin
		if(ten_thousands >= 5)
		ten_thousands = ten_thousands + 3;
		if(thousands >= 5)
			thousands = thousands + 3;
		if(hundreds >= 5)
			hundreds = hundreds + 3;
		if(tens >= 5)
			tens = tens + 3;		
		if(ones >= 5)
			ones = ones + 3;		

		ten_thousands = ten_thousands << 1; 
		ten_thousands[0] = thousands[3];	
		thousands = thousands << 1;
		thousands[0] = hundreds[3];		
		hundreds = hundreds << 1;
		hundreds[0] = tens[3];
		tens = tens << 1;
		tens[0]= ones[3];
		ones = ones << 1;
		ones[0] = hex_reg[15];
		hex_reg = {hex_reg[14:0], 1'b0};
	end
end

Referring to Figure 7.2, the former part of the program is the judgment calculation part, and if it is greater than or equal to 5, then adds 3. The latter part is the shift part.

The third step: verification

Referring to Experiment 6, simulation was performed using ModelSim, and the simulation conditions are set as follows:

initial  begin
	hex = 0 ;	
	repeat (20) begin 
	#10; 
	hex = {$random}%20000;
	#10;
	end 	
end

At the beginning, the 16-bit binary number is equal to 0. The delay is 10 ns. The 16-bit binary number takes a random number less than 20,000. A delay of 10 ns is applied and the process is repeated 20 times.

After the ModelSim is set and the testbench file is added, perform the simulation. The result is shown in Figure 7.3.

Figure 7.3 Simulation for binary to decimal

Remark and reflection:

1. The assignment symbols for the examples above are “=” instead of “<=”. Why?
2. Since the whole program is designed to be combinational logic, when invoking the modules, the other modules should be synchronized the timing.

7.4 Application of Hexadecimal Number to BCD Number Conversion

1. Continue to complete the multiplier of Experiment 6 and display the result on segment display in decimal. Every 1 second, the calculation results on the segment display changes once. The experiment needs to use frequency division, segment display, multiplier and hexadecimal number to BCD number conversion.
2. Compilation. Observe the Timing Analyzer in Compilation Report.
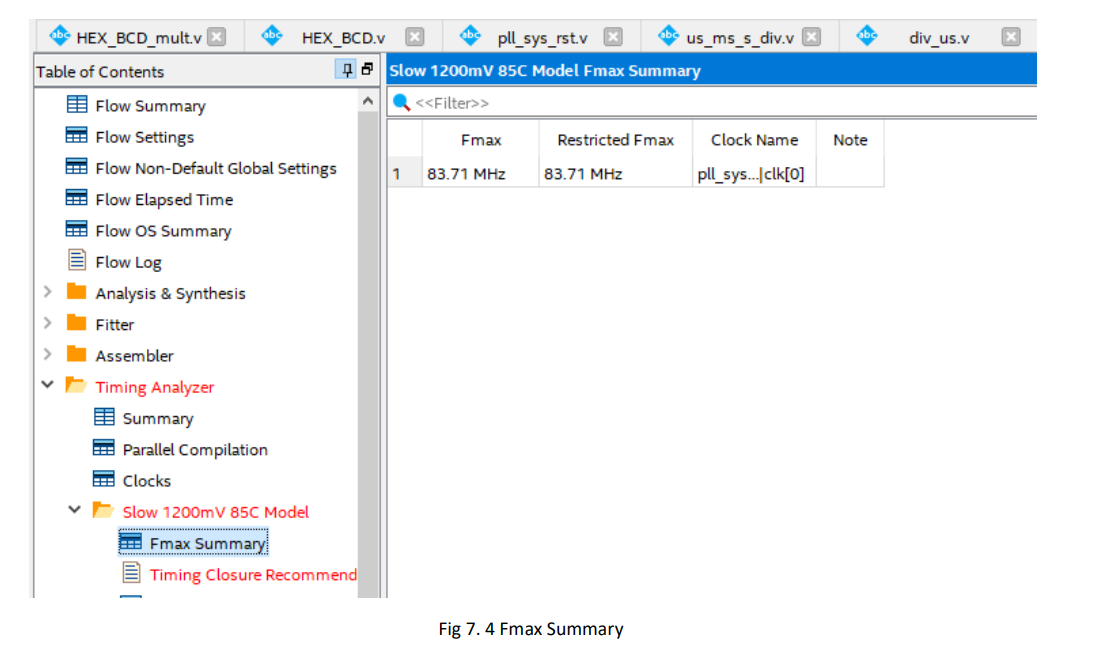
3. Fmax Summary 83.71 MHz. See Figure 7.4.

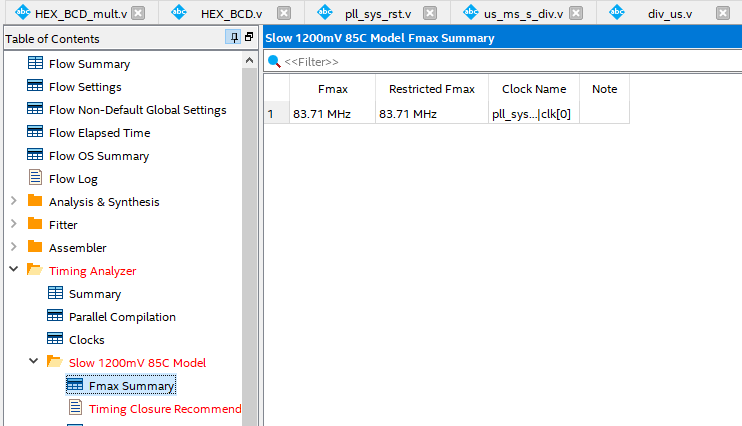
Figure 7.4 Fmax Summary

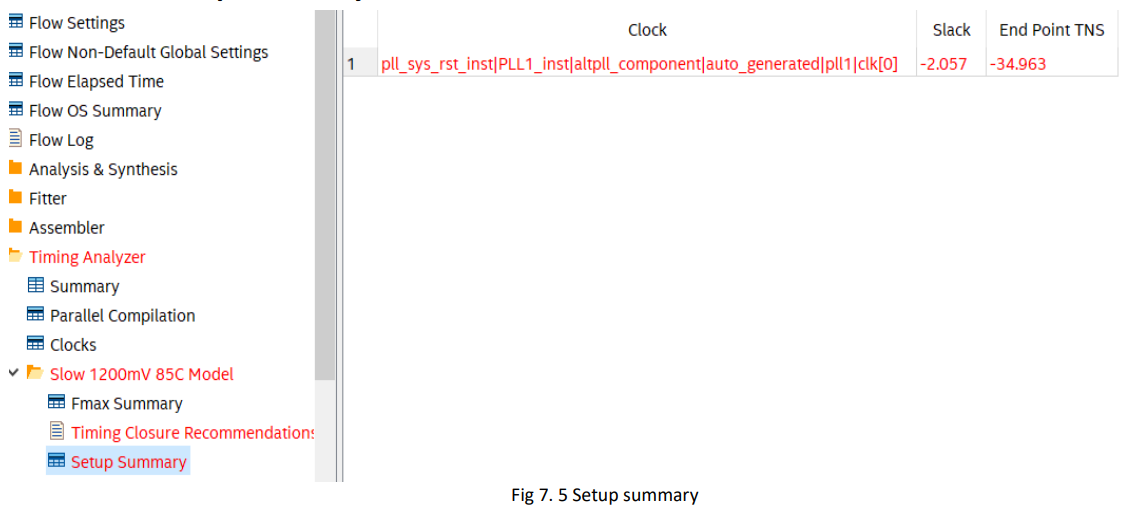
1. Setup Memory

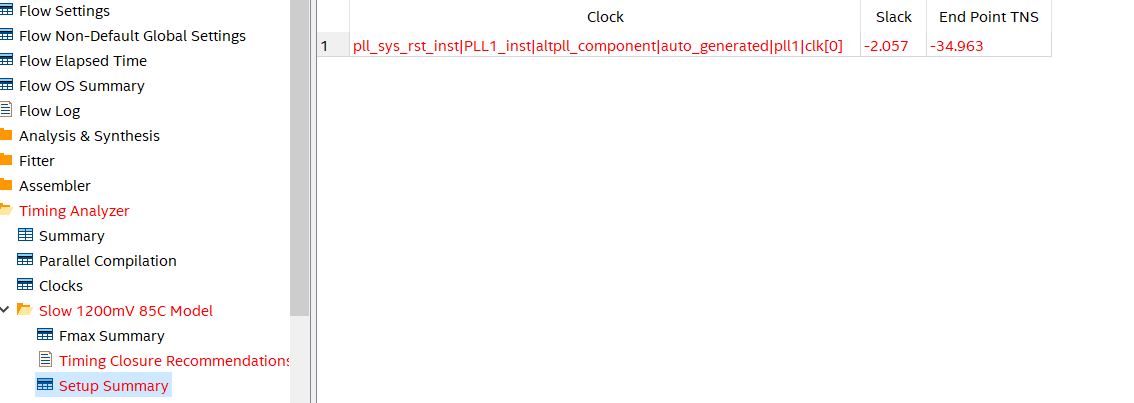
Figure 7.5 Setup time summary

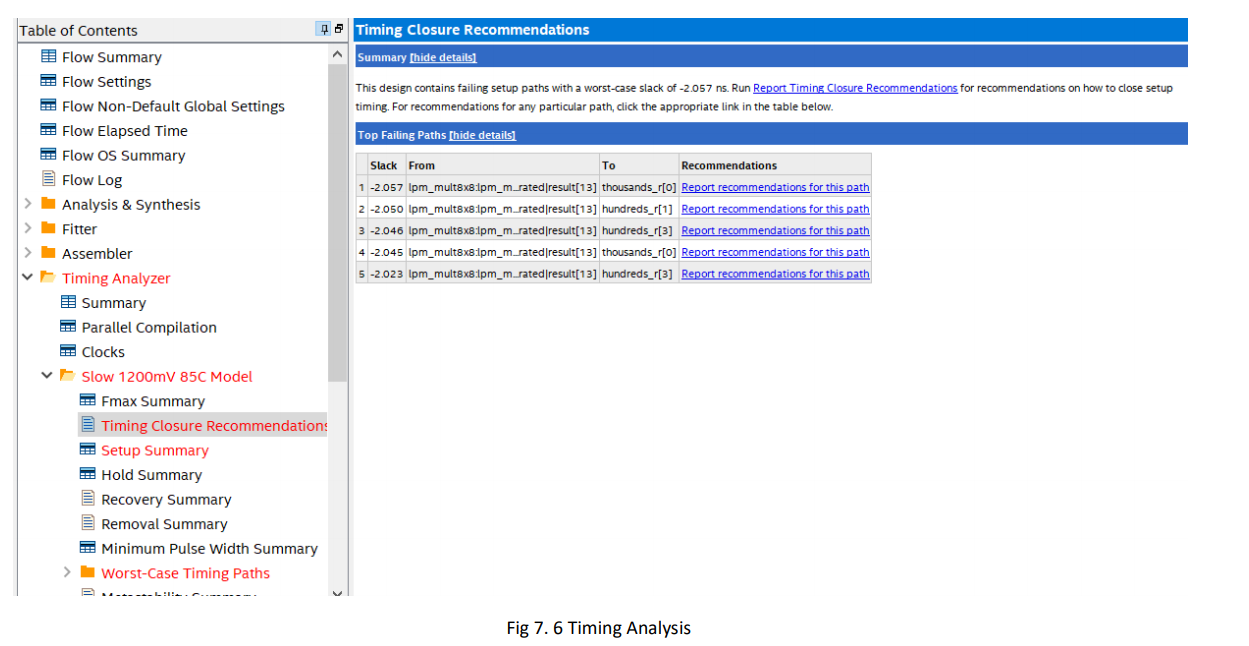
1. Timing Closure Recommendation. See Figure 7.6.

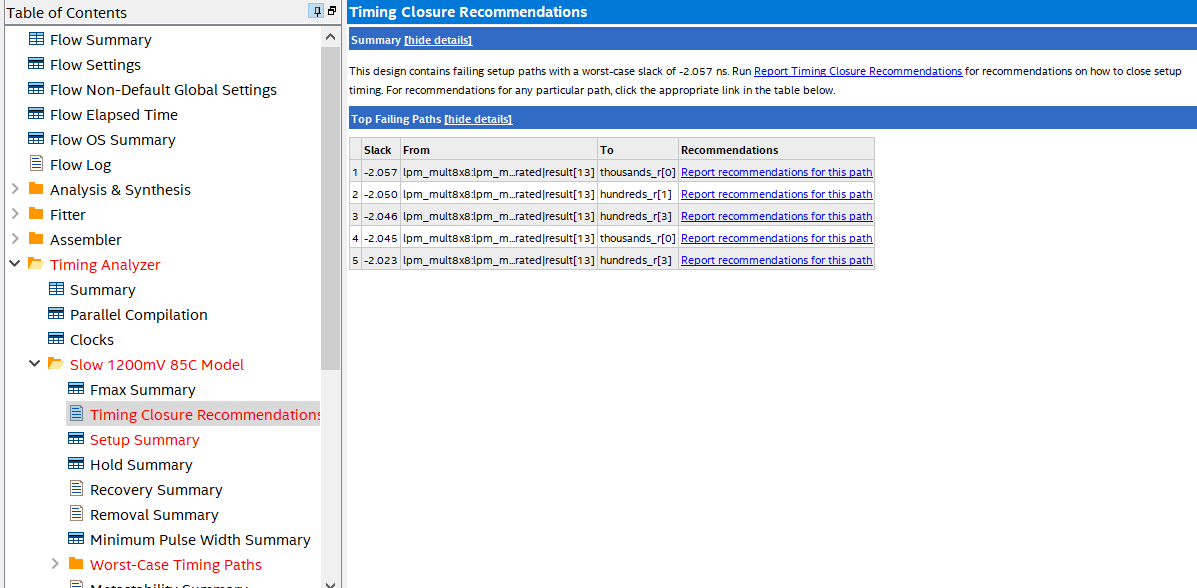
图7-6 Timing Analysis

1. From the above three indicators, the above programming does not meet the timing requirements. It can also be seen that the maximum delay path is the delay of the output of the multiplier to HEX_BCD.

There are 3 solutions:

1. Reduce the clock frequency
2. Increase the timing of HEX_BCD and increase the pipeline
3. Insert pipeline isolation at the periphery (can reduce some delay)

The way to increase the pipeline, will be introduced in the follow-up experiment, because the function of HEX_BCD is mainly used to display the human-machine interface, the speed requirement is low, and the frequency reduction method is adopted here.

1. Modify PLL to increase an output of 20 MHz frequency (BCD_clk)
2. Recompile and observe timing results
3. Lock the pins, compile, and program FII-PRA040 development board for testing

7.5 Experiment Verification

The first step: pin assignment

See Table 7.1 for the pin assignment

Table 7.1 Hexadecimal to BCD number conversion pin mapping

Signal Name	Network Label	FPGA Pin	Port Description
clk	C10_50MCLK	91	Input clock
rst	KEY3	10	Reset
scan[5]	SEG_3V3_D5	124	Bit selection 5
scan[4]	SEG_3V3_D4	127	Bit selection 4
scan[3]	SEG_3V3_D3	129	Bit selection 3
scan[2]	SEG_3V3_D2	141	Bit selection 2
scan[1]	SEG_3V3_D1	142	Bit selection 1
scan[0]	SEG_3V3_D0	136	Bit selection 0
seven_seg[7]	SEG_PA	128	Segment selection a
seven_seg[6]	SEG_PB	135	Segment selection b
seven_seg[5]	SEG_PC	138	Segment selection c
seven_seg[4]	SEG_PD	126	Segment selection d
seven_seg[3]	SEG_PE	125	Segment selection e
seven_seg[2]	SEG_PF	133	Segment selection f
seven_seg[1]	SEG_PG	137	Segment selection g
seven_seg[0]	SEG_DP	132	Segment selection dp
SW[7]	SW7_LED7	77	Switch 7
SW[6]	SW6_LED6	76	Switch 6
SW[5]	SW5_LED5	75	Switch 5
SW[4]	SW4_LED4	74	Switch 4
SW[3]	SW3_LED3	87	Switch 3
SW[2]	SW2_LED2	86	Switch 2
SW[1]	SW1_LED1	83	Switch 1
SW[0]	SW0_LED0	80	Switch 0

The second step: development board verification

After the pin assignment is completed, the compilation is performed. Program the development board for verification after passing. The experimental result is shown in Figure 7.7. The value of the DIP switch input is 00001010, decimal 10, the counter is constantly accumulating, so the display result is always accumulatively changed by 10.

Figure 7.7 Experiment phenomenon

Experiment Summary and Reflection

1. How to implement BCD using more than 16 bits binary numbers
2. What is a synchronous clock and how to handle an asynchronous clock
3. Learn to design circuits that meet timing requirements based on actual needs.

———————————————————————-

---

Old Version (2019 )

7.1 Experiment Objective

1. Convert binary numbers to BCD
2. Convert hexadecimal numbers to BCD

7.2 Experiment Principle

1. Since the hexadecimal display is not intuitive, decimal display is more widely used in real life.

2. Human eyes recognition is relatively slow, so the display from hexadecimal to decimal does not need to be too fast. Generally, there are two methods

  a. Countdown method:

Under the control of the synchronous clock, the hexadecimal number is decremented by 1 until it is reduced to 0. At the same time, the appropriate BCD code decimal counter is designed to increment. When the hexadecimal number is reduced to 0, the BCD counter just gets with the same value to display.

b. Bitwise operations (specifically, shift bits and plus 3 here). The implementation is as follows:

1. 1. Set the maximum decimal value of the expression. Suppose you want to convert the 16-digit binary value (4-digit hexadecimal) to decimal. The maximum value can be expressed as 65535. First define five four-digit binary units: ten thousand, thousand, hundred, ten, and one to accommodate calculation results

   2. Shift the hexadecimal number by one to the left, and put the removed part into the defined variable, and judge whether the units of ten thousand, thousand, hundred, ten, and one are greater than or equal to 5, and if so, add the corresponding bit to 3 until the 16-bit shift is completed, and the corresponding result is obtained.

Note: Do not add 3 when moving to the last digit, put the operation result directly

1. 3. The principle of hexadecimal number to BCD number conversion. Suppose ABCD is a 4-digit binary number (possibly ones, 10 or 100 bits, etc.), adjusts it to BCD code. Since the entire calculation is implemented in successive shifts, ABCDE is obtained after shifting one bit (E is from low displacement and its value is either 0 or 1). At this time, it should be judged whether the value is greater than or equal to 10. If so, the value is increased by 6 to adjust it to within 10, and the carry is shifted to the upper 4-bit BCD code. Here, the pre-movement adjustment is used to first determine whether ABCD is greater than or equal to 5 (half of 10), and if it is greater than 5, add 3 (half of 6) and then shift.  For example, ABCD = 0110 (decimal 6)

1) After shifting it becomes 1100 (12), greater than 1001 (decimal 9)

2) By plus 0110 (decimal 6), ABCD = 0010, carry position is 1, the result is expressed as decimal 12

3) Use pre-shift processing, ABCD = 0110 (6), greater than 5, plus 3

4) ABCD = 1001 (9), shift left by one

5) ABCD = 0010, the shifted shift is the lowest bit of the high four-bit BCD.

6) Since the shifted bit is 1, ABCD = 0010(2), the result is also 12 in decimal.

7) The two results are the same

8) Firstly, make a judgement, and then add 3 and shift. If there are multiple BCD codes at the same time, then multiple BCD numbers all must first determine whether need to add 2 and then shift.

3. The first way is relatively easy. Here, the second method is mainly introduced.

Example 1: Binary to BCD

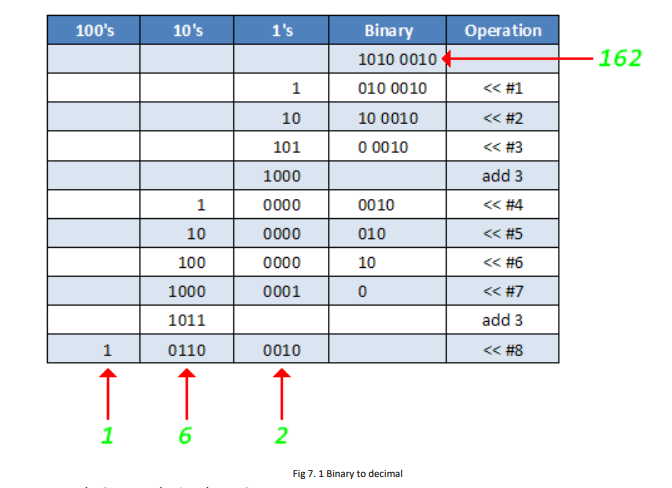
Fig 7. 1 Binary to decimal

Example 2: Hexadecimal to BCD

 

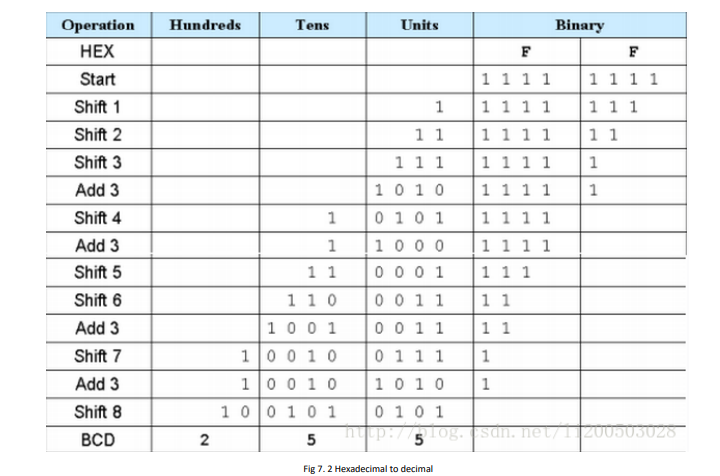
Fig 7. 2 Hexadecimal to decimal

4. Write a Verilog HDL to convert 16-bit binary to BCD. (You can find reference in the project folder, HEX_BCD.v.
5. ModelSim simulation

1. 1. 1. Refer to Experiment 6 to set the simulation
      2. The simulation result is shown in Fig 7. 3

   

Fig 7. 3 Simulation for binary to decimal

6. Remark

The assignment marks for the examples above are “=” instead of “<=”. Why?

Since the whole program is designed to be combinational logic, when invoking the modules, the other modules should be synchronized the timing.

7.3 Application of Hexadecimal Number to BCD Number Conversion

1. Continue to complete the multiplier of Experiment 6 and display the result in segment decoders in decimal. Refer to the attached project file HEX_BCD_mult.v.

2. Compilation. Observe the Timing Analyzer in Compilation Report.

   1. Slow 1200mV 85C Model > Fmax Summary is 83. 71 MHz. See Fig 7. 4

      

Fig 7. 4 Fmax Summary

1. 2. Setup Summary

      

Fig 7. 5 Setup summary

1. 3. Timing Closure Recommendation. See Fig 7. 6

      

Fig 7. 6 Timing Analysis

1. 4. From the above three indicators, the above programming does not meet the timing requirements. It can also be seen that the maximum delay path is the delay of the output of the multiplier to HEX_BCD.

There are 3 solutions:

1. 1. 1. 1. 1. 1. 1. 1. 1. Reduce the clock frequency

                        2. Increase the timing of HEX_BCD and increase the pipeline

                        3. Insert pipeline isolation at the periphery (can reduce some delay)

The way to increase the pipeline, will be introduced in the follow-up experiment, because the function of HEX_BCD is mainly used to display the human-machine interface, the speed requirement is low, and the frequency reduction method is adopted here.

3. Modify PLL to increase an output of 20 MHz frequency.

module pll_sys_rst(
input inclk,
output sys_clk,
output BCD_clk,
output reg sys_rst =1'b1
);
wire pll_locked;
always@(posedge sys_clk)
sys_rst <= !pll_locked;
PLL PLL_inst (
.areset (1'b0),
.inclk0 (inclk),
.c0 (sys_clk),
.c1 (BCD_clk), //20Mhz
.locked (pll_locked)
);
endmodule

4. New code added. Refer to the project files.

reg [15:0] mult_res_r;
always @ (posedge BCD_clk)
mult_res_r<=mult_res;

5. Recompile and observe the timing result.
6. Lock the pins and download the program to FII-PRA010 board. Test it.

7.4 Experiment Summary and Reflection

 

1. How to implement BCD using more than 16bits binary numbers
2. What is a synchronous clock and how to handle an asynchronous clock
3. Learn to design circuits meeting the requirement